科普 | 数学分析在夜景照明设计中的应用|科协频道

科普 | 数学分析在夜景照明设计中的应用

Abstract:

In the field of nightscape lighting design, designers often rely too heavily on intuitive design, neglecting the importance of rational design, leading to significant discrepancies between the actual results of the project and the initial design expectations. This article uses mathematical analysis to calculate the voltage drop of linear lights and the effective spot size of pattern lights in two specific scenarios, thereby highlighting the necessity of rational lighting design.

摘要：

设计师在夜景照明设计工作中存在感性设计多，理性设计少的问题，以至于后期项目落地与前期方案效果有较大偏差。本文通过两个小场景，运用数学分析方法，计算线型灯电压降、图案灯有效光斑大小，认识到理性照明设计的必要性。

Keywords:

voltage drop; spot size; rational lighting design; mathematical analysis; multi-scale relations

关键词：

电压降；光斑大小；理性照明设计；数学分析；多尺度关系

前言

夜景照明设计主要由方案设计+施工图设计两部分组成。本文重点介绍根据方案效果，进行施工图落地的相关部分。电气施工图主要包含灯具选型，设备配电，强弱电控制，安装大样等。目前设计师在设计工作中更多的是凭经验，无尺度关系慨念，只有少数设计师使用模拟软件做相关试验。例如在DIALUX EVO软件中,户外场景的模拟计算结果是否可靠，还需有待考证。软件本身并非存在技术缺陷，而是结果的可靠性需要很多前提条件，例如现场的多尺度关系，周围环境光亮度，IES文件的真实性，被照面的颜色与反射率等是影响计算结果的主要因素。在实际工作中，设计师往往很难准确采集现场数据，从而导致更多是凭经验设计。从数学分析的角度，本文具体分析两个小场景（DC24V线型灯电压降计算、图案灯斜投倾斜屋面光斑计算），以此为例，我们在夜景照明设计中多一些理性，少一些感性。

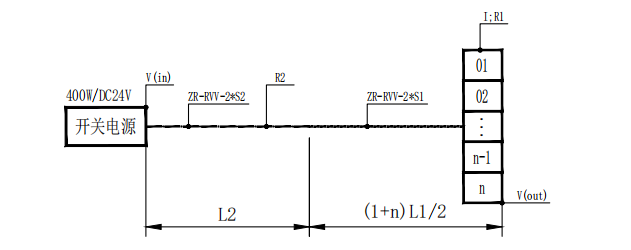
_{单端供电方式电压降拓扑图,见图1。根据欧姆定律，电压=电流*电阻，U=I*R,计算电压降∆U，求解尾灯输出电压}V_out=V_in_-∆U。

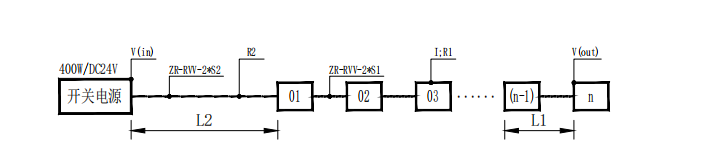
▲图1 单端供电-线型灯电压降拓扑图

V_in_{:输入电压（开关电源输出电压），24V;}

V_out_{:尾灯输出电压，V;}

I:单灯电流，A；

n:单端级联灯具数量，套；

_L₁_{:灯点间距，m；}

_L₂_{:开关电源至首灯距离，m；}

_R₁_{:灯点电源线阻值，Ω/m；}

_R₂_{:开关电源至首灯电源线阻值，Ω/m；}

^_S^₁^{_{:灯点电源线线径，m}}²^_；

^_S^₂^{_{:开关电源至首灯电源线线径，m}}²^_；

对于直流电系统，∆U=IR,R=ρL/S

第n套灯产生的电压降

_∆U_n_=∆U_L2_+∆U_nL1

_=I(ρ2L₂_/S₂_)+I(ρ2nL₁_/S₁₎

_=I(2L₂_R₂_)+I(2nL₁_R₁₎

_=2I(L₂_R₂_+nL₁_R₁_)①

n套灯总电压降

_∆U=∆U₁_+∆U₂_++∆U₃_+...+∆U_n-1_+∆U_n

_=2I[(L₂_R₂_+L₁_R₁_)+(L₂_R₂_+2L₁_R₁_)+...+(L₂_R₂_+(n-1)L₁_R₁_)+(L₂_R₂_+nL₁_R₁_)]

_=2I[nL₂_R₂_+L₁_R₁_{(1+2+...+(n-1)+n)]}

_=2I[nL₂_R₂_+L₁_R₁_n(1+n)/2]

_=nI[2L₂_R₂_+L₁_R₁_(1+n)]②

n尾灯输出电压

V_out=V_in_-∆U③

_{根据GB/T50034-2004采用安全特低电压供电的照明不宜低于其额定电压的90% ,即最大允许降压10%，需满足}V_out_≥21.6V。

_R₁_,R₂_{参数值，可根据电源线线径查询表1（铜线常用产品导体电阻参照表）可得。}

^{_{实际工程中，R}}^₁^_,R^₂^{_{经典值如下：R1=0.0195Ω/m(RVV,S}}^₁^_=1m²^_),

^_R^₂^{_{=0.00495Ω/m(RVV,S}}^₂^_=4m²^_)。

常规情况下，左右两端带灯点数量相等，即对称,见图2 。

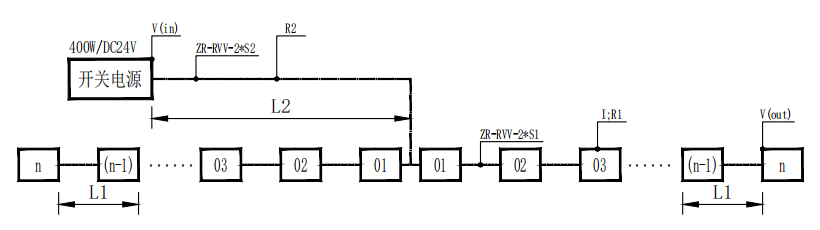
▲图2 两端供电对称-线型灯电压降拓扑图

两端供电方式电压降计算方式与单端供电方式类似，可等效为单端供电方式，开关电源至首灯距离L₂加倍，2L₂，见图3；

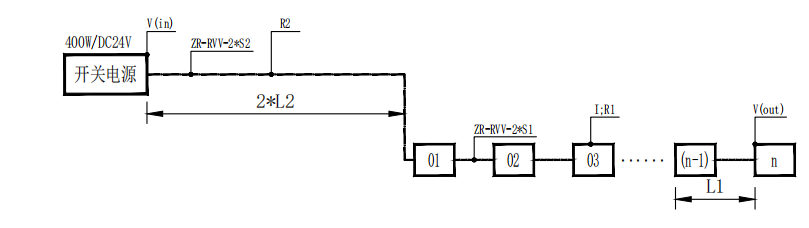
▲图3 两端供电对称-线型灯等效单端供电电压降拓扑图

带入公式①②③

第n套灯产生的电压降

∆U_n=∆U_L2+∆U_nL1=2I(2L₂R₂+nL₁R₁)④

n套灯总电压降，

∆U==nI[4L₂R₂+L₁R₁(1+n)]⑤

n尾灯输出电压

V_out=V_in-∆U⑥

需满足V_out≥21.6V即可。

特殊情况下，左右两端带灯点数量不相等(右端n套，左端m套，n≥m），即非对称,见图4 。

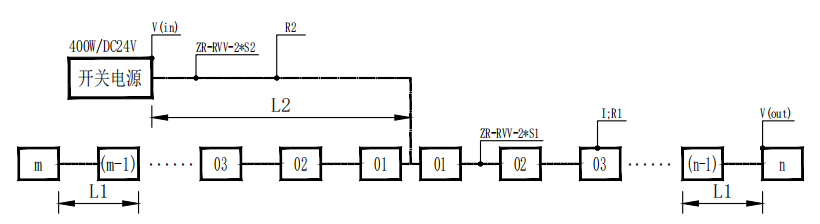
▲图4 两端供电非对称-线型灯电压降拓扑图

根据公式②，

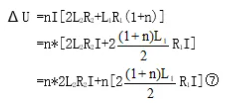
电压降等效为n套灯点在电源线L₂电压降+n套灯点在灯具部分电压降，等效拓扑图，见图5。

▲图5 单端供电-线型灯电压降等效拓扑图

由此可得，两端供电非对称方式等效拓扑图，见图6。

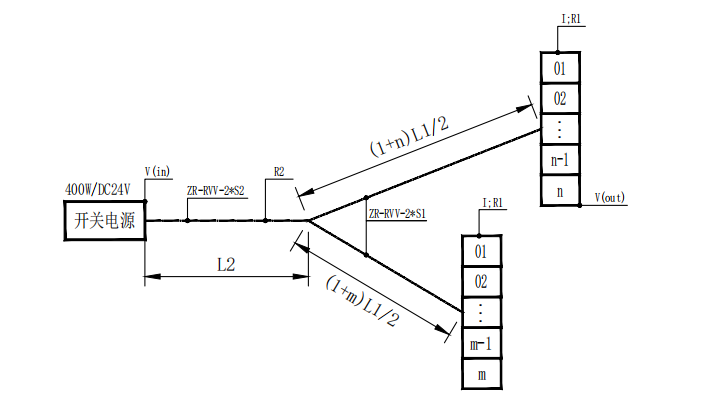
▲图6 单端供电非对称-线型灯电压降等效拓扑图

电压降等效为n+m套灯点在电源线L₂电压降+n套灯点在灯具部分电压降，

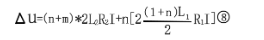
n尾灯输出电压

V_out=V_in-∆U⑨

需满足V_out≥21.6V即可。

在图案灯斜投倾斜屋顶场景中，我们如何分析有效光斑大小，并初步计算呢？存在相对复杂的空间结构，有较多的尺度关系，有两个倾斜，一是灯杆斜投，二是被投面是倾斜的（灯杆与被投面非垂直关系），见图7~10。等效为倾斜正投方案是解决问题的核心方法，见图12，需要在斜屋面所在平面中找到等效灯杆的位置及尺度关系见图11，正投即灯杆与被投面为垂直关系。

我们需要采集现场的真实数据，复原现场模型，这是数学分析的关键所在。实际工作中往往存在两个维度方向：1已知光斑大小，灯杆尺度关系（高度及位置），求灯具参数（光通量、角度）；2已知灯具参数（光通量、角度），灯杆尺度关系（高度及位置），求光斑大小。其实二者本质是一样的，是两种不同表现方式，我们本次按方式2分析计算光斑大小。

需要采集的参数：

_房屋宽度w₁_,长度L₁_；

_{屋面前边缘高度}H_1；

屋面倾斜角度θ；

_{(屋脊底部高度}H₂_，tanθ=(H₂_-H_1)/(w₁_{/2)，θ=arctanθ得到) ；}

需要提出需求参数：

_{光斑中心离屋面两个边缘距离}w₃_和L₃_；

目标光斑大小∅；

_{意愿的灯杆高度}H₃_；

_{意愿的灯杆向外偏移}L₂_{和向前偏移}w₂_；

需要换算出来目标数值：

灯具到屋斜面垂直距离（等效灯杆高度）H；

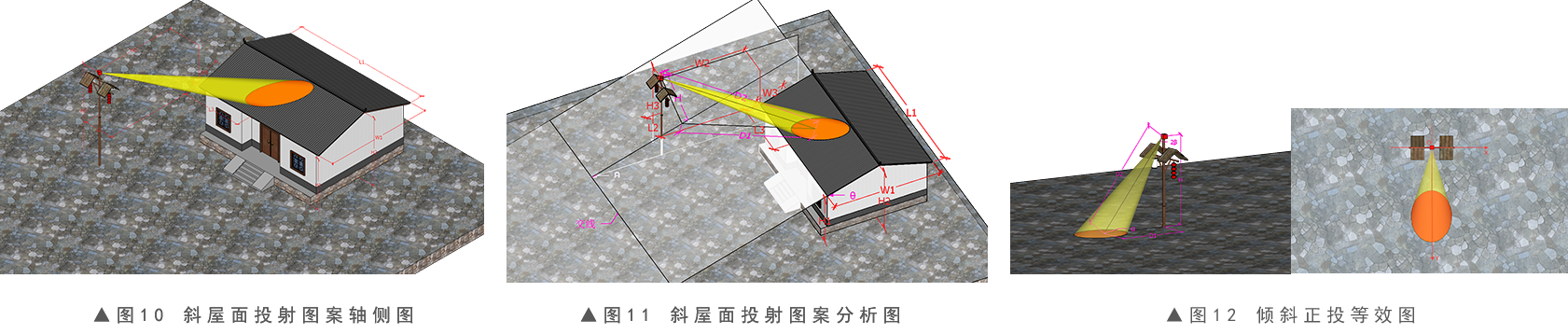
_{灯具在屋斜面的垂足到光斑中心距离}D₁_；

_{灯具到光斑中心（投射点）距离(投距)}D₂_；

参数采集与分析完毕,见图13~14。

_{Rt△AHF中，AH=}H_1/tanθ；

_{Rt△ABC中，AB=AH-BH=}H_1/tanθ-w₂_；

_{→BC=ABtanθ=（}H_1/tanθ-w₂_）tanθ；

Rt△DEC中，DC=DB-CB=H₃-（H₁/tanθ-W₂）tanθ；

→灯具到屋斜面垂直距离

H=DE=DCcosθ

₌₍H_3-（H_1/tanθ-W₂_{）tanθ)cosθ}

₌H_3cosθ-（H_1/tanθ-W₂_）sinθ⑩,

等效灯杆高度H，变矮了：

_CE=DCsinθ=(H_3-（H_1/tanθ-W₂_{）tanθ)sinθ；}

_CF=BH/cosθ=W₂_{/cosθ ,}

_EF=CF-CE=W_2/cosθ-CE

_→EG=EF+FG=W_2/cosθ+W_3-CE;

_GO=L₂₊L₃_,

_{→灯具在屋斜面垂足E到光斑中心O距离}D₁_,

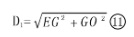
_{→灯具到光斑中心O（投射点）距离(投距)}D₂_,

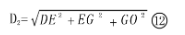
等效为倾斜正投方案，见图12。

_{已知尺度关系H,}D₁_,D₂_{，灯具光束角为2β；}

_{→灯具主光轴与被投面的夹角arctanα=arctan(H/}D₁₎

则有效光斑的边界曲线为

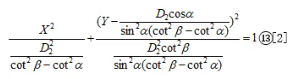
由边界曲线方程可知，光斑是个椭圆，光斑中心沿着Y轴方向有所偏移，非主光轴投射点O；

投射最大有效圆形光斑直径为短轴长度。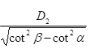

灯杆安装在交线后侧与2.1基本一致，唯一不同之处，在于等效灯杆高度计算，见图15~17。

_{Rt△AHF中，AH=}H₁_/tanθ；

_{Rt△ABC中，AB=BH-AH=}W₂-H₁_/tanθ；

_{→BC=ABtanθ=（}W₂-H₁_{/tanθ）tanθ；}

Rt△DEC中，

_DC=DB+BC=H₃_+（W₂-H₁_{/tanθ）tanθ；}

→灯具到屋斜面垂直距离,

H=DE=DCcosθ

₌₍H₃_+（W₂-H₁_{/tanθ）tanθ)cosθ}

₌H₃_cosθ+（W₂-H₁_{/tanθ）sinθ⑭}

等效灯杆高度H，变高了,

_CE=DCsinθ=(H₃_+（W₂-H₁_{/tanθ）tanθ)sinθ；}

_CF=BH/cosθ=W₂_{/cosθ ,}

_EF=CF-CE=W₂_/cosθ-CE

→EG=EF+FG=W₂/cosθ+W₃-CE;

_GO=L₂+L₃_,

_{→灯具在屋斜面垂足E到光斑中心O距离}D₁_，

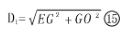
_{→灯具到光斑中心O（投射点）距离(投距)}D₂_，

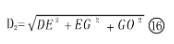
等效为倾斜正投方案，见图12。

有效光斑的边界曲线仍为式⑬。

通过以上两个关于夜景照明小场景数学分析，我们认识到夜景照明设计更多是理性设计，理性设计是感性设计的基石。在场景1( DC24V线型灯电压降计算)中，数学分析适用的前提条件：a恒流灯具;b灯具分线盒中间出线或线型灯PCB版带背线（电源线）；c不适用恒功率灯具。电压降计算的目的是保证最后一名（尾灯）及格，而非保证第一名（首灯）及格即可。我们需要找到最不利尾灯，确定电源线及灯具部分电气路由，根据场景选择对应式③⑤⑧，计算并校验电压降≤10%。在场景2( 图案灯斜投倾斜屋面光斑计算)中，我们首先采集所需参数，然后建立数学模型，转化为空间立体几何的数学分析模型，计算出等效方案的尺度关系（H，D₁，D₂），最后由式⑬计算出有效光斑大小。倾斜屋面与水平地面的交线是分界线，灯杆安装在分界线的前侧和后侧计算方式略有不同，但最终都需等效为倾斜正投方案。灯杆安装在分界线前侧，等效灯杆变矮了，反之变高了，所以我们优先选择在分界线后侧安装灯杆，这样有利于节省成本。灯杆安装在分界线后侧会导致投距D₂相对变大，在保证被照面照度恒定的前提下，需要增加灯具光通量；被照面材质也需要重点关心，如颜色，反射率等。现场的尺度关系是影响落地效果的重要因素之一，我们需综合考虑其他因素，寻求最大的平衡点。

参考文献

[1] 《多尺度照明应用方法论》. 韩柏光.广州朗文光电有限公司

[2] （226）斜面截圆锥面所得曲线是椭圆的推导过程,黄老师聊数学. 黄剑航

活动报名

科普 | 数学分析在夜景照明设计中的应用